Kuhn length

The Kuhn length is a theoretical treatment, developed by Werner Kuhn, in which a real polymer chain is considered as a collection of N Kuhn segments each with a Kuhn length b. Each Kuhn segment can be thought of as if they are freely jointed with each other.[1][2][3] Each segment in a freely jointed chain can randomly orient in any direction without the influence of any forces, independent of the directions taken by other segments. Thus the real chain consisting of n bonds and with fixed bond angles and bond lengths is replaced by an equivalent chain with N connected Kuhn segments that can orient in any random direction. 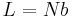The length of a fully stretched chain or the contour length is L=Nb for the Kuhn segment chain. In the simplest treatment, such a chain follows the random walk model, where each step taken in a random direction is independent of the directions taken in the previous steps, forming a random coil. The average end-to-end distance for a chain satisfying the random walk model is 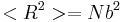<R^2> = Nb^2. Since the space occupied by a segment in the polymer chain cannot be taken by another segment, a self-avoiding random walk model can also be used. The Kuhn segment construction is useful in that it allows complicated polymers to be treated with simplified models as either a random walk or a self-avoiding walk, which can simplify the treatment considerably.

For an actual homopolymer chain (consists of the same repeat units) with bond length 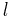l and bond angle θ with a dihedral angle energy potential, the average end-to-end distance can be obtained as 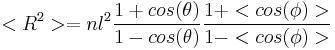<R^2> = nl^2 {{1%2Bcos(\theta )} \over{1-cos(\theta)}}{{1%2B<cos(\textstyle\phi\,\!)>} \over{1-<cos (\textstyle\phi\,\!)>}} , where 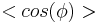<cos (\textstyle\phi\,\!)> is the average cosine of the dihedral angle. Also the fully stretched length 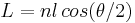L = nl\, cos(\theta/2). By equating 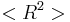<R^2> and L for the actual chain and the equivalent chain with Kuhn segments, the number of Kuhn segments N and the Kuhn segment length b can be obtained.

For semiflexible chain, Kuhn length equals two times the persistence length [4].

References

  1. ^ Flory, P.J. (1953) Principles of Polymer Chemistry, Cornell Univ. Press, ISBN 0-8014-0134-8
  2. ^ Flory, P.J. (1969) Statistical Mechanics of Chain Molecules, Wiley, ISBN 0-470-26495-0; reissued 1989, ISBN 1-56990-019-1
  3. ^ Rubinstein, M., Colby, R. H. (2003)Polymer Physics, Oxford University Press, ISBN 0-19-852059-X
  4. ^ Gert R. Strobl (2007) The physics of polymers: concepts for understanding their structures and behavior, Springer, ISBN 3540252789